1. Come si calcola la volatilità annua
Maggiore è la volatilità, maggiore è l’incertezza attesa, motivo per cui questo indicatore è tra i più utilizzati per misurare il rischio finanziario.
Ad esempio, se un ETF ha una volatilità annua del 2%, significa che, supponendo una distribuzione normale dei rendimenti, questi tenderanno a fluttuare in media di ±2% rispetto al rendimento atteso.
Come si calcola la deviazione standard annuale (volatilità)
Nelle informazioni sui singoli asset si parla indifferentemente di volatilità annua o di deviazione standard, sempre su base annuale.
Per calcolare correttamente la volatilità, servono più rendimenti annuali storici possibili.
Il procedimento è:
-
Calcolare la media dei rendimenti annui.
-
Calcolare, per ciascun anno, lo scarto dalla media.
- Sommare tutti gli scarti quadrati.
-
Dividere per (n - 1) (con (n) numero di anni): si ottiene la varianza campionaria.
-
Estrarre la radice quadrata della varianza: è la deviazione standard, ovvero la volatilità.
Es: ETF obbligazionario (rendimento 2%, volatilità 2%)
Media dei rendimenti annui: (0,67 - 0,52 + 2,75 + 4,67 + 2,43) / 5 = 2%
Scarti dalla media: −1,33%, −2,52%, +0,75%, +2,67%, +0,43%
Somma scarti quadrati: 1,77 + 6,35 + 0,56 + 7,13 + 0,18 = 15,99
Varianza: 15,99 / (5-1) = 4
Deviazione standard (volatilità): √ 4 = 2%
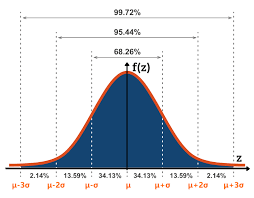
Significa che hai una probabilità del:
- 68,26% che il rendimento sia tra 0% (2% − 2%) e 4% (2% + 2%)
-
95,44% che il rendimento sia tra −2% (2% − 2×2%) e 6% (2% + 2×2%)
-
99,72% che il rendimento sia tra −4% (2% − 3×2%) e 8% (2% + 3×2%)
Attenzione:
- Il rendimento è espresso in termini nominali ovvero al lordo d'imposte e inflazione. Al netto di tutto tenderà allo 0.
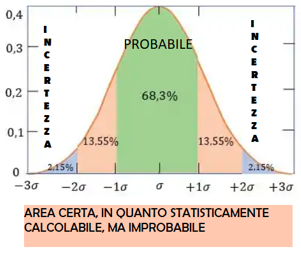
- L’intervallo al 95,44% lascia fuori un 4,56% di probabilità. Questa si divide tra eventi molto positivi (destra) e molto negativi (sinistra).
Le code di sinistra, che rappresentano eventi distruttivi (perdita di lavoro, invalidità, morte), non si gestiscono con la finanza, ma con coperture assicurative, previdenziali e assistenziali.
Es: ETF azionario globale (rendimento 6%, volatilità 12%)
Media dei rendimenti annui: (18,13 + 11,39 - 13,35 + 3,47 + 10,36) / 5 = 6%
Scarti dalla media: +12,13%, +5,39%, −19,35%, −2,53%, +4,36%
Somma scarti quadrati: 147,14 + 29,06 + 374,36 + 6,40 + 19,01 = 575,9
Varianza: 575,97 / (5-1) = 143,99
Deviazione standard (volatilità): √ 143,99 = 12,00%
Significa che hai una probabilità del:
-
68,26% che il rendimento sia tra −6% (6% − 12%) e +18% (6% + 12%)
-
95,44% tra −18% (6% − 2×12%) e +30% (6% + 2×12%)
-
99,72% tra −30% (6% − 3×12%) e +42% (6% + 3×12%)
2. Come incide il tempo sulla volatilità
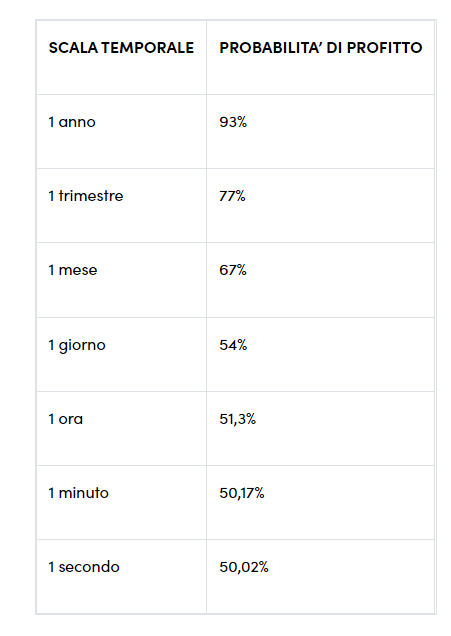
Su orizzonti temporali più lunghi la volatilità tende a "diluire" le fluttuazioni [1], anche se il rischio che l'asset subisca un crollo temporaneo all’interno del periodo considerato rimane invariato.
La volatilità a un anno è facilmente reperibile, poiché viene generalmente indicata nelle schede informative dei singoli strumenti finanziari. Tuttavia, stimare la volatilità su orizzonti temporali più estesi è molto più complesso, perché raramente è disponibile in modo diretto. Di conseguenza, è necessario calcolarla autonomamente..

Si creano dei "periodi mobili" che corrispondono all'orizzonte temporale scelto, nel nostro caso 5 anni. Sono intervalli temporali consecutivi di uguale durata che si sovrappongono parzialmente tra loro. L'orizzonte temporale corrisponde al periodo nel quale rischi di perdere parte del tuo capitale e di non reggere emotivamente l'apnea finanziaria ovvero la momentanea perdita rispetto al capitale iniziale.
Ora rileviamo i rendimenti annualizzati del nostro investimento su tutte le finestre temporali.
Ipotizziamo che siano uguali all'esempio precedente, solo che al posto di "Rendimenti annui" abbiamo i rendimenti dei singoli periodi mobili:
Media dei rendimenti dei singoli periodi mobili: (18,13 + 11,39 - 13,35 + 3,47 + 10,36) / 5 = 6%
Scarti dalla media: +12,13%, +5,39%, −19,35%, −2,53%, +4,36%
Somma scarti quadrati: 147,14 + 29,06 + 374,36 + 6,40 + 19,01 = 575,9
Varianza: 575,97 / (5-1) = 143,99
Deviazione standard (volatilità): √ 143,99 = 12,00%
La volatilità sarà uguale all'esempio precedente con l'orizzonte temporale ad un anno ma con un orizzonte temporale più lungo varierà la volatilità cumulata.
Ora, per chiarire meglio l’effetto teorico del tempo, immaginiamo sempre il caso semplificato, ma realistico analizzato in precedenza: un investimento che offre un rendimento annuo composto atteso del 6% e una volatilità annua costante del 12%.
Come varia la volatilità in un orizzonte temporale di 5 e 20 anni
La volatilità annua misura la dispersione dei rendimenti attorno alla media in un singolo anno. Ma se consideriamo periodi più lunghi, come 5 o 20 anni, dobbiamo calcolare la volatilità cumulata, che cresce secondo la radice quadrata del tempo:
Volatilità su T anni = Volatilità annua x √ T
Nel nostro caso:
- Dopo 1 anno: 12%
-
Dopo 5 anni: 12% x √ 5 ≃ 26,83%
-
Dopo 20 anni: 12% x √20 ≃ 53,66%
Significa che l’intervallo dei possibili risultati si allarga nel lungo periodo, ma non in modo lineare: raddoppiare il tempo non raddoppia la volatilità, la aumenta meno.
Investimento iniziale di 100 €,
rendimento atteso 6% annuo e volatilità annua 12%
🔹 Dopo 5 anni:
- Valore atteso: 134,99 €
- Intervallo di confidenza al 68%: tra 99,57 € e 170,29 €
- Intervallo di confidenza al 95%: tra 76,14 € e 222,70 €
🔹 Dopo 20 anni:
- Valore atteso: 332,01 €
- Intervallo di confidenza al 68%: tra 168,09 € e 491,68 €
- Intervallo di confidenza al 95%: tra 98,28 € e 840,91 €
Il risultato è che nel lungo periodo:
-
La forbice tra rendimento minimo e massimo si allarga, ma…
-
…la probabilità di un risultato positivo diventa sempre più alta.
In altre parole, il tempo diluisce la volatilità per anno e amplifica i benefici del rendimento atteso.
Questa è una delle ragioni fondamentali per cui gli investimenti azionari sono consigliabili su orizzonti temporali lunghi, nonostante la volatilità iniziale.
Riprendiamo ora lo stesso esercizio teorico, ma immagina che il rendimento reale, cioè al netto delle imposte e dell'inflazione, riducesse il rendimento medio annuo composto al 3% netto, ma con la stessa volatilità annua del 12%.
Investimento iniziale di 100 €,
rendimento atteso 3% annuo e volatilità annua 12%
🔹 Dopo 5 anni:
- Valore atteso: 116,18 €
- Intervallo al 68%: tra 85,70 € e 146,57 €
- Intervallo al 95%: tra 65,53 € e 191,68 €
🔹 Dopo 20 anni:
- Valore atteso: 182,21 €
- Intervallo al 68%: tra 92,25 € e 269,84 €
- Intervallo al 95%: tra 53,94 € e 461,50 €
Anche in questo scenario, l’investimento diventa tanto più vantaggioso quanto più lungo è l’orizzonte temporale, perché le probabilità che il capitale superi le imposte e l’inflazione aumentano.
Chi investe in strumenti volatili ma con un rendimento reale positivo deve accettare l’instabilità di breve, ma viene premiato nel lungo periodo.
3. Come incide la diversificazione
La diversificazione, che consiste nell'investire in strumenti differenti (azioni, obbligazioni, immobili, materie prime, criptovalute, ecc.), riduce il rischio complessivo di un portafoglio. Poiché i rendimenti degli asset non sono perfettamente correlati, la diversificazione attenua l'impatto di perdite significative su singoli asset.
Ti ricordiamo che:
-
la media aritmetica è la somma dei rendimenti divisa per il numero degli anni. Non tiene conto della sequenza dei rendimenti.
-
la media geometrica è quella che misura quanto è cresciuto realmente il tuo capitale nel tempo, tenendo conto della capitalizzazione composta (cioè l’effetto dell’interesse sugli interessi). È sempre più bassa della media aritmetica quando c’è volatilità.
Per questa ragione:
-
Un investimento molto volatile può avere alti rendimenti in alcuni anni, ma se poi scende drasticamente, la perdita pesa più del guadagno equivalente.
-
Un portafoglio diversificato riduce questi sbalzi e consente di evitare le grandi perdite, che sono molto più difficili da recuperare.
Esempio con un singolo titolo, hai 100 euro:
-
Anno 1: guadagni +50% ⇒ hai 150 euro
-
Anno 2: perdi -50% ⇒ 150 × 0,5 = 75 euro
- Media aritmetica: (50% + (-50%)) / 2 = 0% come se il titolo fosse rimasto stabile per due anni.
Ma hai perso soldi: sei passato da 100 a 75 euro. - Media geometrica ≈ -13% annuo (perché 100 → 75 in 2 anni)
Esempio con un portafoglio volatile:
-
-
Anno 1: +60% → da 100 a 160 €
-
Anno 2: -55% → da 160 a 72 €
-
Media aritmetica: +2,5%
-
Media geometrica (reale): -15,15%
Nonostante la media aritmetica sia positiva, hai perso il 28% del capitale iniziale.
Esempio con un portafoglio diversificato:
-
-
Anno 1: +4% → da 100 a 104 €
-
Anno 2: +1% → da 104 a 105,04 €
-
Media aritmetica: +2,5% (come nell'esempio del portafoglio volatile)
-
Media geometrica: +2,49%
-
Capitale finale: 105,04 €
-
Hai guadagnato circa il 5% sul capitale iniziale, con rendimenti stabili.
-
Quando diversifichi, riduci le oscillazioni forti (volatilità). E questo fa sì che il rendimento reale nel tempo (media geometrica) sia più alto rispetto a un investimento molto volatile, anche se in media (aritmetica) potrebbe sembrare uguale.
4. Volatilità negativa (da evitare)
Quella che distrugge valore, come negli esempi visti prima:
-
Forti perdite seguite da alti guadagni (o viceversa), che ridimensionano la media geometrica;
-
Mancanza di diversificazione, che espone a eventi estremi su singoli asset.
→ È la volatilità non gestita, che non premia, ma punisce nel lungo termine, come nell'assunzione di rischi specifici collegati ad investimenti in singoli titoli.
5. Volatilità benefica (principio guida n°1)
Quella che può generare rendimento, se affrontata con una strategia consapevole:
-
Riguarda portafogli ben diversificati ma esposti a classi di attivo con volatilità e potenziale di rendimento maggiore, come le azioni;
-
Lavora nel tempo grazie alla legge dei grandi numeri: con il reinvestimento dei profitti e una strategia costante, le oscillazioni di mercato offrono occasioni di crescita (principio guida n°2: orizzonte temporale);
-
Richiede tempo e disciplina, non panico.
Un investimento più volatile tende a offrire rendimenti potenzialmente più elevati, per compensare il rischio maggiore assunto dagli investitori.
La volatilità, dunque, comporta un percorso decisamente più accidentato, ma anche la possibilità di ottenere profitti più elevati.
Questo fenomeno si fonda sulla legge dei grandi numeri: nel lungo periodo, le oscillazioni di mercato tendono a bilanciarsi, favorendo gli investitori che adottano una strategia dinamica e coerente nel tempo.
Questa volatilità benefica:
- È una volatilità che porta a evoluzione, apprendimento, miglioramento del sistema.
- È associata a fenomeni come l’antifragilità (concetto di Nassim Taleb), dove piccole perturbazioni rafforzano un sistema invece di distruggerlo;
- Sistemi antifragili → Beneficiano di piccole variazioni e usano la volatilità a proprio vantaggio (es. evoluzione biologica, adattamento dei mercati).
- Matematicamente, si può modellare con distribuzioni scalabili, dove eventi piccoli sono frequenti e aiutano il sistema ad adattarsi.
- Esempi: piccole fluttuazioni nei mercati che portano a opportunità di investimento, stress controllato nel corpo umano che rafforza la resilienza.
6. Volatilità letale
- È una volatilità che causa collasso o danni irreparabili;
- È caratterizzata da eventi estremi, spesso descritti dalle code pesanti della distribuzione di Pareto o della distribuzione di Lévy, dove eventi rari e catastrofici hanno un impatto enorme;
La diversificazione serve a contenere la volatilità distruttiva.
Questa volatilità è tipica nei sistemi fragili → Sono sensibili a grandi variazioni e possono collassare rapidamente (es. una banca con alta leva finanziaria). Esempi: crisi finanziarie sistemiche, terremoti distruttivi, shock biologici letali.
7. Cause della volatilità
L’aumento della volatilità dipende dai seguenti rischi:
- Episodico: caratterizzato da eventi di rischio di breve durata, il cui carattere transitorio spesso è evidente soltanto a posteriori. Un episodio significativo si è verificato nell’agosto 2024, quando i segnali di indebolimento del mercato del lavoro americano, unitamente alla chiusura delle posizioni in carry trade, hanno provocato un’impennata della volatilità che si è riassorbita già nella settimana successiva.
- Legato al ciclo economico: un aumento della volatilità legato a un rallentamento economico e al timore di una recessione. La recessione del 2001 negli Stati Uniti dopo lo scoppio della bolla delle dot-com è un esempio tipico.
- Esistenziale: la prospettiva di un crollo sistemico dell’economia e/o del sistema finanziario. Questo è un tipo di rischio che si manifesta con estrema rarità. La crisi finanziaria globale del 2008–2009 e la fase iniziale della pandemia di Covid-19 nel 2020 sono due esempi.
8. Rapporto tra rendimento e volatilità: l'indice di Sharpe
L'indice di Sharpe valuta il rendimento aggiustato per il rischio di un investimento.
Si calcola utilizzando la seguente formula:
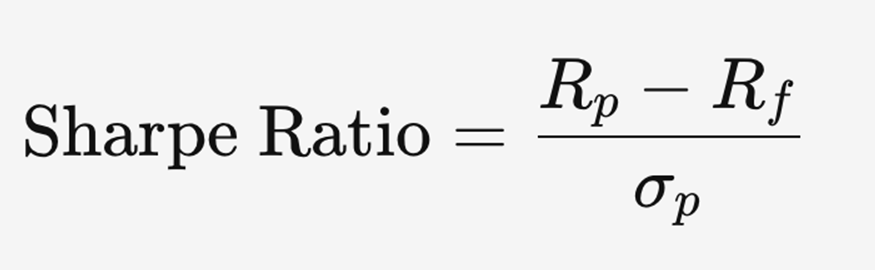
dove:
– ( R_p) è il rendimento atteso del portafoglio o dell’investimento.
– ( R_f) è il rendimento di un’attività priva di rischio, come i titoli di stato.
– ( sigma_p) è la deviazione standard dei rendimenti del portafoglio, che rappresenta la volatilità.
Il rendimento storico considerato può variare a seconda dell’analisi, ma spesso si utilizza un periodo annuale per ( R_p).
La volatilità storica (sigma_p) è anch’essa calcolata solitamente su base annua.
Non c’è un valore massimo per l’Indice di Sharpe; teoricamente, più alto è l’indice, migliore è il rendimento aggiustato per il rischio ottenuto. Un valore negativo indica che il rendimento del portafoglio è inferiore al rendimento dell’attività priva di rischio. Un valore di 1 o superiore è generalmente considerato accettabile, mentre un valore di 2 o superiore è considerato eccellente.
COLLEGAMENTO TRA VOLATILITA’ LETALE / BENEFCA E L’INDICE DI SHARPE
L’indice di Sharpe utilizza la volatilità totale, senza distinguere tra la volatilità benefica (che porta a guadagni) e la volatilità letale (che porta a perdite). Tuttavia, possiamo analizzare come Sharpe si collega a questi due tipi di volatilità:
A – Volatilità benefica e Indice di Sharpe
- Se la volatilità è dovuta a oscillazioni contenute e controllate, il portafoglio può adattarsi ai cambiamenti del mercato, sfruttando le opportunità di guadagno;
- Se il rendimento cresce più della volatilità, allora Sharpe aumenta, indicando un miglioramento dell’efficienza del portafoglio.
B – Volatilità letale e Indice di Sharpe
- Se la volatilità proviene da eventi estremi e imprevedibili (crisi finanziarie, crolli di mercato), i drawdown distruggono i rendimenti.
- In questo caso, Sharpe diminuisce drasticamente, segnalando un aumento del rischio non compensato da adeguati guadagni;
- Gli eventi letali sono spesso descritti da code pesanti (modelli di distribuzione di Lévy o Pareto) e rendono inefficaci le strategie di ottimizzazione basate sulla deviazione standard;
- Esempio pratico: investimenti con alta leva finanziaria in mercati illiquidi (es. LTCM nel 1998) → elevati Sharpe ex-ante, ma vulnerabilità a volatilità letale.
COME GESTIRE LE DUE VOLATILITA’ NELL’INDICE DI SHARPE
L’INDICE DI SORTINO
L’Indice di Sortino è una metrica di performance che rappresenta una variante dell'Indice di Sharpe, ma con una differenza fondamentale: distingue tra la volatilità positiva (benefica) e negativa (letale) permettendo di:
- Premiare gli asset che beneficiano di piccole variazioni.
- Penalizzare le strategie fragili esposte a grandi crolli di mercato.
Approcci alternativi:
- Value at Risk (VaR) e Expected Shortfall (ES) → misurano il rischio di eventi estremi.
- Modelli asimmetrici GARCH → distinguono tra volatilità positiva e negativa.
L’indice di Sharpe non distingue tra volatilità benefica e letale, ma può essere integrato con metriche come l’indice di Sortino per valutare meglio il rischio asimmetrico. Investire in asset antifragili riduce la volatilità letale e aumenta il rapporto rischio/rendimento, migliorando l’indice di Sharpe nel lungo termine.
9. Considerazioni finali
-
La volatilità annua misura il rischio di un investimento su base annuale, calcolata come deviazione standard dei rendimenti storici.
-
Il rischio annualizzato tende a diminuire con l'aumentare dell'orizzonte temporale, ma lungo il percorso di investimento possono comunque verificarsi drawdown profondi e persistenti.
-
La diversificazione riduce il rischio complessivo di portafoglio, mitigando l'impatto delle oscillazioni negative su singoli asset e aumentando la probabilità di ottenere rendimenti positivi nel lungo periodo.
-
Un portafoglio ben strutturato:
-
limita gli effetti delle perdite significative (geometria del rendimento),
-
ma accetta e include una quota di rischio per beneficiare della crescita nel tempo.
-