Il sogno di tutti è scegliere un portafoglio sapendo con certezza quanto potrà performare in un certo numero di anni. Sapendolo sarebbe facile scegliere la migliore asset allocation.

In questo paragrafo te lo spieghiamo.

Ma attenzione, sapere quanto performerà il tuo capitale alla fine dell'orizzonte temporale che hai scelto, non esclude, seppur temporaneamente,  di perdere gran parte del tuo denaro durante il percorso.

Per questa ragione il tuo consulente finanziario indipendente  dovrà aitarti a decidere il tuo orizzonte temporale ideale: quello che puoi sopportare, non tanto finanziariamente ma piuttosto emotivamente.

Ora che ti è chiaro questo concetto puoi decidere il tuo orizzonte temporale, cioè il numero di anni in cui potresti perdere parte del tuo capitale, e decidere l'asset allocation che ti conviene di più.

Abbiamo scelto questi due periodi / orizzonti temporali in quanto se devi disporre con certezza del tuo denaro dopo 1 o 3 anni sai già che non puoi che indirizzarti verso un Portafoglio sicurezza stracolmo di obbligazioni che, nel migliore delle ipotesi, riusciranno a mantenere invariato il potere d'acquisto del tuo investimento. 

ORIZZONTE TEMPORALE A 5 ANNI

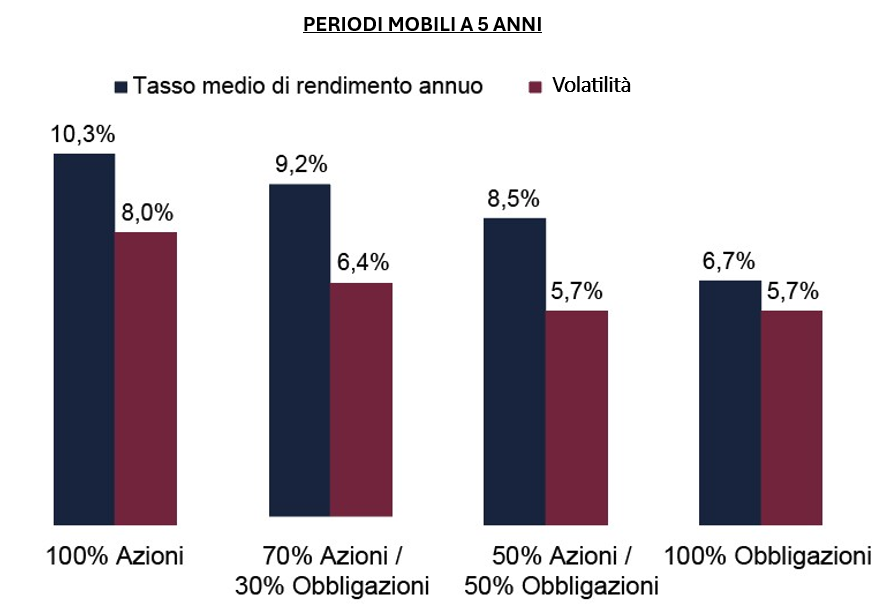
Fonte: Global Financial Data, Inc. (GFD) in base ai rendimenti medi in periodi mobili a 5 anni in base ai rendimenti dell’indice GFD’s World dal 1926 al 2018.

Il portafoglio con il 100% in azioni offre un rendimento nettamente superiore, mentre il portafoglio con il 100% in obbligazioni presenta una volatilità molto più contenuta.

Ora ti tocca fare uno sforzo mentale per tradurre in qualcosa cosa di concreto queste informazioni, al fine di scegliere la migliore asset allocation consapevolmente. Consapevolezza necessaria per non cambiare strategia al momento sbagliato.

Non fare caso ai rendimenti su cui operiamo, che sono elevati rispetto a quelli realizzabili nei prossimi anni, principalmente a causa dell'inflazione, ma questo non inficerà il risultato finale.  

100% azionario su 5 anni

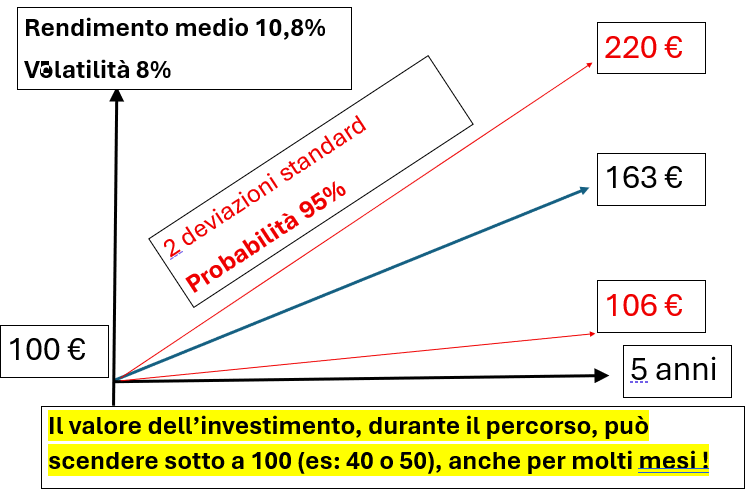
Avendo investito 100 € al 100% in azioni, con un rendimento del 10,3% (vedi grafico), mediamente, sottolineo mediamente, dopo 5 anni avresti maturato circa 163 €, ma, il tuo problema, è che potrebbe non essere sempre così. Dunque, andremo a calcolare quali probabilità hai di avere periodi di 5 anni buoni o cattivi e di quantificarne le conseguenze in termini di guadagni o di perdite.

Nel grafico sopra, che stiamo interpretando, leggiamo, nella seconda colonna, che la volatilità è stata dell'8% ma dobbiamo comprendere come è stato calcolata, diversamente sarebbe un numero senza significato. 

Lo spieghiamo con un esempio:

I "periodi mobili" corrispondono all'orizzonte temporale scelto, nel nostro caso 5 anni. Sono intervalli temporali consecutivi di uguale durata che si sovrappongono parzialmente tra loro. Corrispondono al tempo nel quale rischi di perdere parte del tuo capitale e di non reggere emotivamente l'apnea finanziaria.

Gli anni esemplificati nelle colonne della tabella sono 10 per semplicità: avremmo dovuto prevederne 93, in quanto la nostra serie storica a disposizione è fortunatamente più lunga e sicura, in quanto va dal 1926 al 2018. Anche i periodi (righe) sono solo 5 ma avremmo dovuto indicarne 89.

Ora rileviamo i rendimenti annualizzati del nostro investimento su tutte le finestre temporali:

1926-1930    10,3%

1927-1931    0,5%

1928-1932    4,7%

1929-1933    15,9%

1930-1934    20,1%

....

2014-2018    ....%

Sin qui è una rilevazione storica, lunga ma semplice da comprendere, che noi abbiamo abbreviato per semplicità; ora andiamo a calcolare la volatilità (cioè la % che rappresenta la deviazione standard).

Passo 1: Calcolare la media dei rendimenti annualizzati

(10,3 + 0,5 + 4,7 + 15,9 + 20,1) / 5 = 51,5 / 5 = 10,3%, che corrisponde alla prima colonna del grafico.

Stiamo facendo sempre l'esercizio su 5 anni anziché 89 (in 93 anni ci sono 89 periodi mobili di 5 anni). 

Passo 2: Calcolare la deviazione standard (volatilità)

Calcoliamo:

• la differenza di ogni rendimento dalla media
• il quadrato di queste differenze

1926-1930: resa 10,3% - 10,3% =  0 al quadrato 0

1927-1931: resa 0,5% - 10,3% = -9,8  al quadrato 96,04

1928-1932: resa 4,7% - 10,3% =  -5,6 al quadrato 31,36

1929-1933: resa 15,9% - 10,3% = 5,6 al quadrato 31,36

1930-1934: resa 20,1% - 10,3% =  9,8  al quadrato 96,04

• Somma dei quadrati: 0 + 96,04 + 31,36 + 31,36 + 96,04 = 254,8

• Dividiamo per il (numero degli anni - 1) = 5 - 1 = 4  ⇒ 254,8 / 4 = 63,7

• Radice quadrata √ di 63,7 per ottenere la volatilità: 8% che corrisponde alla seconda colonna del grafico, per il caso dell'asset 100% azionario. Questo significa che, guardando a periodi di 5 anni, i rendimenti medi annualizzati di questo investimento tendono a variare del ±8 % intorno alla media del 10,3%.

Questa distribuzione di rendimenti mostra chiaramente come un portafoglio completamente azionario possa offrire rendimenti potenzialmente molto elevati (fino al 20,1%), ma anche risultati significativamente inferiori alla media (scendendo fino allo 0,5%), confermando l'alta volatilità di questo tipo di investimento rappresentato nel grafico.

Ora che abbiamo compreso cosa è la volatilità possiamo misurarla calcolando la deviazione standard (σ sigma minuscola). Si calcola con questa formula:   

σ 5 anni = volatilità 8% × √5 anni ≈ 17,9%

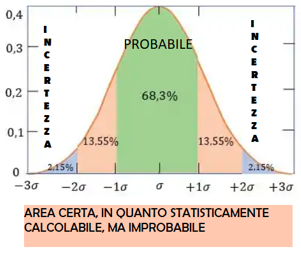
Siamo arrivati al risultato che cercavamo, infatti, assumendo una distribuzione normale dei rendimenti, così come ci ha insegnato il matematico e fisico tedesco Carl Friedrich Gauss (che prendiamo per buono in quanto dovremmo fare l'intero corso di laure di statistica), hai circa:

• Il 68% di probabilità di ottenere un risultato compreso tra:  163 × (1−0,179) = 134 €  e 163 ×(1+0,179) =192 €

• Il 95% di probabilità di ottenere un risultato compreso tra: 163×(1− 2 × 0,179) = 106 € e $€$

In sintesi, dopo 5 anni con rendimento medio del 10,3% e volatilità annua dell’8%, il capitale atteso è 163 €, ma con una probabilità del 68% il risultato sarà tra 134 € e 192 €, e con una probabilità del 95% sarà tra 106 € e 220 €.

Ti residuerà il 2,15% di probabilità che diventi miliardario ed un 2,15% che scoppi una guerra atomica ma, in entrambi i casi, non dovrai preoccuparti troppo.

100% obbligazionario su 5 anni

Avendo investito 100 € al 100% in obbligazioni, mediamente dopo 5 anni avresti maturato circa 138 €, ma, anche in questo caso, non è detto che sia sempre così e, dunque, vuoi sapere cosa può accaderti nelle migliori e peggiori ipotesi.

Ora procediamo più spediti senza ripetere il ragionamento visto in predenza.

Su un orizzonte di 5 anni, la deviazione standard dei rendimenti si calcola come: 

σ 5 anni =  volatilità 5,7% × √5 anni ≈ 12,75%

Assumendo una distribuzione normale dei rendimenti, hai circa:

• Il 68% di probabilità di ottenere un risultato compreso tra: 138×(1−0,1275) = 120,5 €   e  138×(1+0,1275) = 155,6 €

• Il 95% di probabilità di ottenere un risultato compreso tra: 138×(1−2×0,1275) = 102,8 €  e 138×(1+2×0,1275) = 173,2

In sintesi, dopo 5 anni con rendimento medio del 6,7% e volatilità annua del 5,7%, il capitale atteso è 138 €, ma con una probabilità del 68% il risultato sarà tra 120,5 € e 155,6 €, e con una probabilità del 95% sarà tra 102,8 € e 173,2 €.

In pratica, su periodi di 5 anni, hai compreso come il 100% azioni performi sempre e comunque meglio del 100% obbligazioni .. atomica a parte.

ORIZZONTE TEMORALE A 20 ANNI

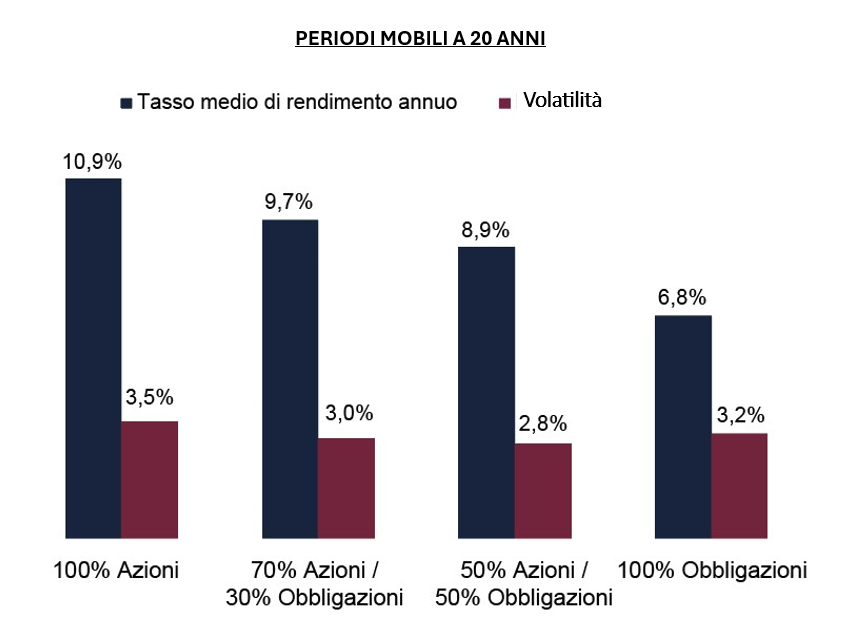
Fonte: Global Financial Data, Inc. (GFD) in base ai rendimenti medi in periodi mobili a 20 anni in base ai rendimenti dell’indice GFD’s World dal 1926 al 2018.

100% azionario su 20 anni

Avendo investito 100 € al 100% in azioni, mediamente dopo 20 anni avresti maturato circa 791 €, ma, ... hai compreso che non è detto che sia sempre così.

Su un orizzonte di 20 anni, la deviazione standard dei rendimenti si calcola come:

σ 20 anni = 3,5% × √20 ≈ 15,65%

Assumendo una distribuzione normale dei rendimenti, hai circa:

• Il 68% di probabilità di ottenere un risultato compreso tra: 791×(1−0,1565) = 667 €  e 791×(1+0,1565) = 915 €

• Il 95% di probabilità di ottenere un risultato compreso tra: 791×(1−2×0,1565) = 543 €   e 791×(1+2×0,1565) =1.039 €

In sintesi, dopo 20 anni con rendimento medio del 10,9% e volatilità annua del 3,5%, il capitale atteso è 791 €, ma con una probabilità del 68% il risultato sarà tra 667 € e 915 €, e con una probabilità del 95% sarà tra 543 € e 1.039 €.

Niente male ma non iniziare a spendere questi denari perché ora devi solo capire come scegliere l'asset allocation ideale, poi dovranno passare 20 anni, devi depurarli dall'inflazione, pagarci il 26% di capital gain, le spese di bollo, ecc. 

100% obbligazionario su 20 anni

Avendo investito 100 € al 100% in obbligazioni, mediamente dopo 20 anni avresti maturato circa 371 €, ma ....

Su un orizzonte di 20 anni, la deviazione standard dei rendimenti si calcola come:

σ 20 anni = 3,2% × √20 ≈ 14,31%

Assumendo una distribuzione normale dei rendimenti, hai circa:

• Il 68% di probabilità di ottenere un risultato compreso tra: 371×(1−0,1431) = 318 €  e $371\times (1+0,1431)=424€$

• Il 95% di probabilità di ottenere un risultato compreso tra: 371×(1−2×0,1431) = 265 €  e  371×(1+2×0,1431) = 477 € 

In sintesi, dopo 20 anni con rendimento medio del 6,8% e volatilità annua del 3,2%, il capitale atteso è 371 €, ma con una probabilità del 68% il risultato sarà tra 318 € e 424 €, e con una probabilità del 95% sarà tra 265 € e 477 €.

In pratica, ragion di più su periodi di 20 anni, hai compreso come il 100% azioni performi sempre e comunque molto meglio del 100% obbligazioni .. sempre atomica a parte.

E' avvenuto il miracolo:

l'orizzonte temporale ha stravolto il risultato!

Su 20 anni il 100% di azionario ha nettamente il maggior rendimento con una volatilità di pochissimo superiore a quella obbligazionaria.

Il 100% di obbligazionario è stato un disastro, la peggior redditività con una volatilità persino superiore ai due portafogli diversificati.

Il principio base di ogni investimento è che la volatilità è il carburante che genera rendimento.

Con un orizzonte temporale lungo come si spera sia quello della tua pensione, le azioni sono meno volatili delle obbligazioni.

LE PREVISIONI DI VANGUARD PER I PROSSIMI 10 ANNI

Passiamo da un backtest secolare alle previsioni dei prossimi 10 anni di Vanguard le conclusioni non sono molto diverse.

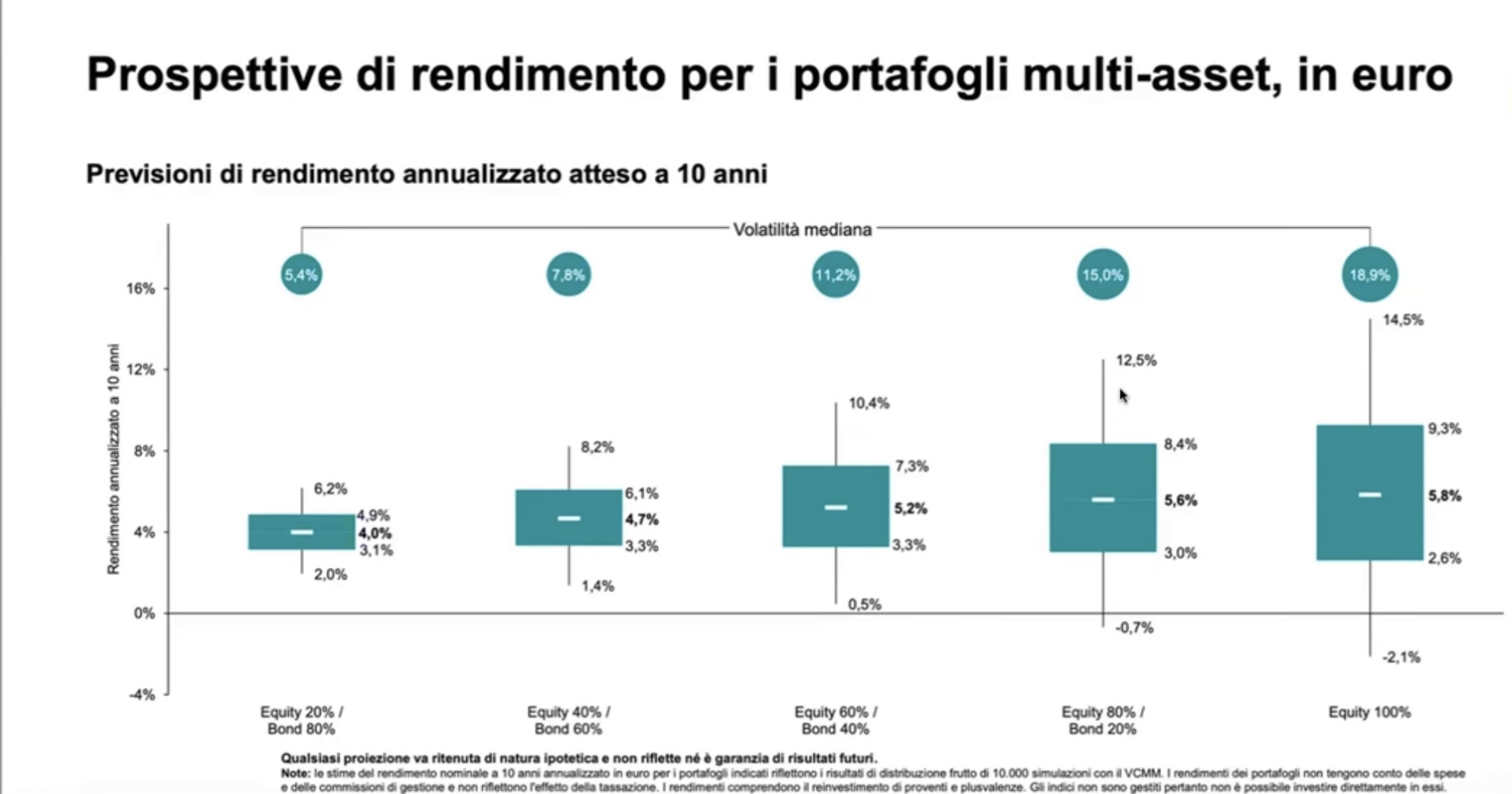
Anche in questo caso la soluzione 60%-40% ti garantisce la "certezza" di non perdere (atomica a parte, con una probabilità del 2,5%) ed un rendimento medio del 5,2%, che non è molto distante dal 5,8% della soluzione con il 100% azioni. Ma quest'ultimo scenario prevede un viaggio decisamente più  ansiolitico (da -2,1% a +14,5% all'anno sempre al lordo d'inflazione, imposte e spese varie). 

Le ragioni economiche 

Nel paragrafo "Strategie d'investimento" potrai ulteriormente scoprire come:

• diversificare e migliorare il tuo rendimento a parità di volatilità 
• diminuire ulteriormente la volatilità a parità di rendimento  

DALLA TEORIA ALLA PRATICA

I sell-off e i drawdown non devono essere solo compresi teoricamente, ma anche vissuti, soprattutto quelli che si protraggono per mesi o anni. Per questo motivo, è consigliabile iniziare il tuo percorso finanziario in modo prudente, per poi costruire gradualmente un portafoglio ideale attraverso una formazione continua, preferibilmente con il supporto del tuo consulente finanziario indipendente.